Circuito Chiuso
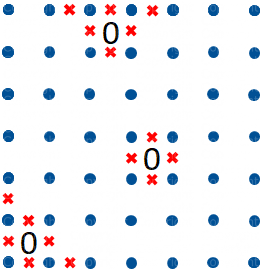
Figura 1
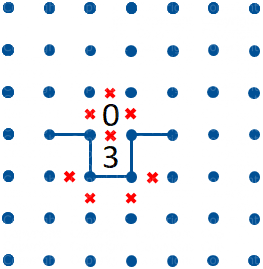
Figura 2
Tecniche di base
Zero
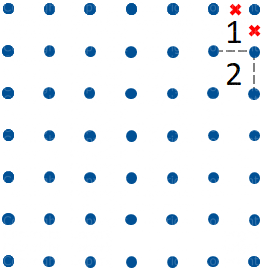
Attorno allo Zero non possono esserci segmenti di percorso. Ma c'è di più: se lo Zero si trova sul bordo o in uno degli angoli del diagramma possiamo senz'altro escludere altri due segmenti di percorso (vd. figura 1).
Zero e Tre ortogonalmente adiacenti
Se uno Zero ed un Tre sono ortogonalmente adiacenti possiamo senz'altro tracciare i segmenti di percorso indicati in figura 2 ed escludere altri quattro segmenti vicini al Tre.
Zero e Tre diagonalmente adiacenti
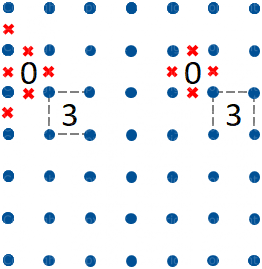
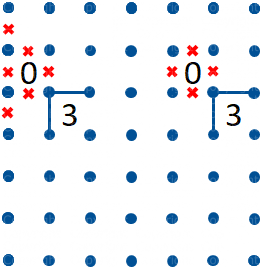
Se uno Zero ed un Tre sono diagonalmente adiacenti abbiamo due percorsi possibili attorno al Tre, indicati in grigio in figura 3. Possiamo pertanto tracciare i segmenti che si ripetono in entrambe le soluzioni, come in figura 4.
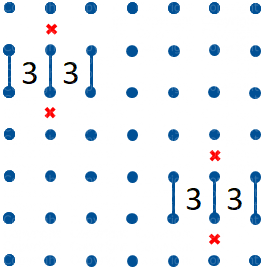
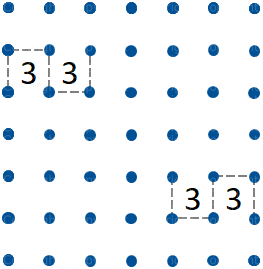
Figura 4
Figura 5
Figura 6
Figura 3
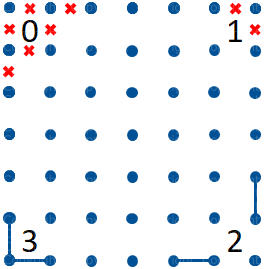
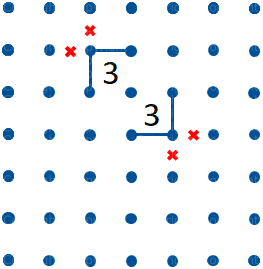
Figura 8
Figura 7
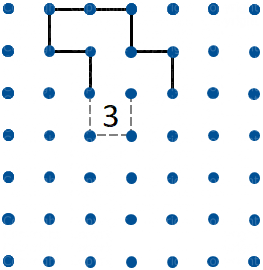
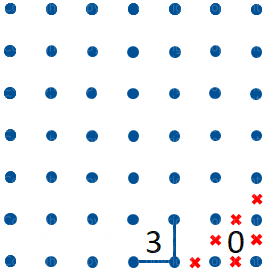
Figura 10
Figura 9
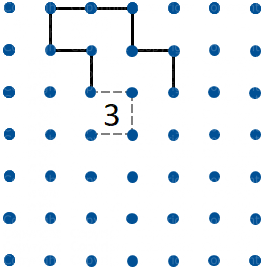
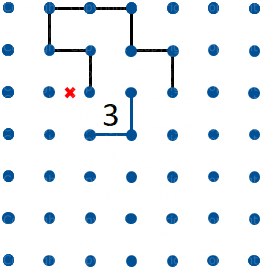
Figura 12
Figura 11
Tre ortogonalmente adiacenti
Se ci sono due Tre ortogonalmente adiacenti esistono solo due possibili percorsi attorno ad essi (vd. figura 5). Possiamo quindi tracciare i tre segmenti comuni ed escludere due segmenti accanto al segmento centrale (vd. figura 6).
Tre diagonalmente adiacenti
Se due Tre sono diagonalmente adiacenti possiamo tracciare senz'altro quattro segmenti ed escluderne altri quattro (vd. figura 7).
Angoli
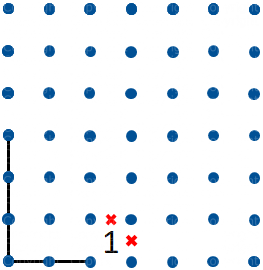
Se abbiamo un Uno nell'angolo dello schema possiamo escludere i due segmenti esterni; se invece abbiamo un Tre nell'angolo possiamo tracciare gli stessi segmenti. Se abbiamo un Due nell'angolo dello schema abbiamo due possibili tracciati: in entrambi i casi possiamo tracciare i segmenti indicati in figura 8.
Tecniche avanzate
Tre e Zero
Quando abbiamo un Tre sul bordo, separato da una casella vuota da uno Zero nell'angolo, allora abbiamo solo due possibili percorsi attorno al Tre e possiamo quindi tracciare i segmenti indicati in figura 9.
Percorso che raggiunge un Tre
Quando abbiamo un percorso che raggiunge un Tre, come in figura 10, abbiamo solo due possibili tracciati attorno al Tre (figure 10 e 11) e possiamo quindi tracciare/escludere i segmenti indicati in figura 12.
Percorso che raggiunge un Uno sul bordo
Quando un percorso raggiunge un Uno sul bordo, come nella situazione in figura 13, possiamo senz'altro escludere i segmenti indicati.
Due adiacente all'Uno nell'angolo
Quando abbiamo un Due ortogonalmente adiacente ad un Uno nell'angolo esistono solo due percorsi possibili attorno al Due (vd. figure 14 e 15) e possiamo quindi tracciare il segmento sul bordo (vd. figura 16).
Percorso chiuso
In figura 17 possiamo escludere i segmenti indicati, altrimenti il percorso si chiuderebbe, senza potersi collegare agli altri segmenti.
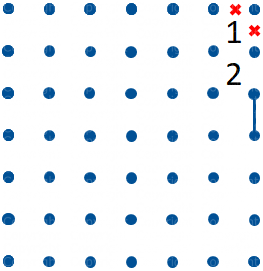
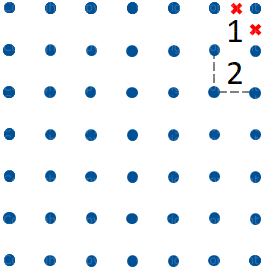
Figura 14
Figura 15
Figura 16
Figura 13
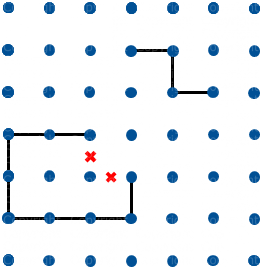
Figura 17
Ultimo aggiornamento: 19/04/2025


